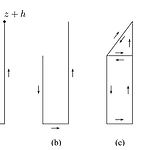
Theorem. open disc에서 holomorphic한 function은 그 disc 안에서 primitive를 가진다.proof. 일반성을 잃지 않고 disc는 원점을 중심으로 한다고 하자.주어진 $z \in D$에 대해 $0$과 $z$를 연결하는 piecewise curve를 고려한다. 그 curve는 0부터 $Re(z)$, $Re(z)$부터 $z$가 이어진 형태이다. 이 polygonal line 을 $\gamma_z$라고 놓자. $$F(z) = \int _{\gamma_z } f(w)dw$$ 로 $F$를 정의했을 때 $D$에서 $F$는 holomorphic이고 $F'=f$을 보이면 충분하다.$z+h \in D$가 되도록 하는 충분히 작은 \(h ..

Theorem. $f$가 entire, bounded 이면 $f$는 constant이다.Remark.entire : $\mathbb{C}$ 전체에서 holomorphic함 bounded : disc으로 덮을 수 있다, 즉 모든 $z$에 대해 $|f(z)|0 , \; z_0 \in \mathbb{C}$에 대해 Cauchy inequalities를 적용하면 $$|f'(z_0 ) | < \frac {B}{R}$$ ($B$는 $f$의 bound), $R \rightarrow \infty$를 취하면 원하던 결과가 쉽게 도출된다.이 theorem으로 간단하게 대수학의 기본 정리를 증명할 수 있다. Corollary. 모든 복소수 계수의 non-constant 다항식 \(P(z) = a..

$f$는 open set $\Omega$에서 holomorphic하다. $D$는 $z_0$를 중심으로 하는 closure가 $\Omega$ 내에 있는 disc일 때, $f$는 $z_0$에서 power series expansion을 가지고 모든 $z \in D$에 대해 계수는 다음과 같다. $$f(z) = \sum _{n=0} ^\infty a_n (z - z_0 )^n , \quad a_n = \frac {f^{(n)}(z_0)}{n!} \; \forall n\ge 0$$ 증명. $z \in D$를 고정하자. Cauchy integral formula에 의해\[ f(z) = \frac {1}{2 \pi i} \int _C \frac {f(\zeta)}{\zeta -z} ..

$f$가 중심이 $z_0$이고 반지름이 $R$인 open disc $D$를 포함하는 open set에서 holomorphic할 때, 다음이 성립한다. $C$는 $D$의 boundary circle이다. $$|f^{(n)} (z_0 ) | \le \frac {n! ||f||_C }{R^n }, \quad ||f||_C := \sup _{z \in C} |f(z)|$$ 증명.Cauchy's integral formula를 사용하면\[ |f^{(n)} (z_0) | = \frac {n!}{2 \pi} \left| \frac {1}{i} \int _C \frac {f(\zeta )}{(\zeta -z_0)^{n+1}} d \zeta \right| = \frac {n!}{2 \pi } \le..

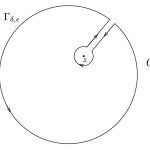
disc $D$의 closure을 포함하는 open set $\Omega \in \mathbb{C}$에 대해 함수 $f$는 holomorphic하다. $C$는 양의 orientation을 가지는 $D$의 boundary circle을 뜻할 때, 모든 점 $z \in D$에 대하여 다음이 성립한다. $$f(z) = \frac {1}{2 \pi i} \int _C \frac {f(\zeta)}{\zeta - z } d\zeta$$ Reference : Princeton Lectures in Analysis$z$를 고정시켰을 때 위 그림과 같은 keyhole $\Gamma _{\delta, \epsilon }$을 고려한다. $\delta$는 구멍에 연결된 통로의 폭, \(\e..

$\gamma$는 open set $\Omega \subset \mathbb{C}$ 내의 closed curve이다. $f$가 $\Omega$에서 continuous이고 primitive를 가질 때 다음이 성립한다. $$\int _\gamma f(z) dz = 0$$ 증명.조금 더 확장시켜서 closed curve은 시작되는 값과 끝나는 값이 같기 때문에 다음을 보이면 충분하다.$\Omega$에서 continuous이고 primitive $F$를 가지는 함수 $f$와 $\Omega$ 내의 $w_1$에서 시작해서 $w_2$로 끝나는 curve $\gamma$에 대해 다음이 성립한다. $$\int _\gamma f(z)dz = F(w_2) - F(w_1)$$ \(\g..

복소수 수열 $\{ x_n \}$이 $w \in \mathbb{C}$에 수렴한다는 것은 다음과 같다는 것을 의미한다. $$\lim _{n \rightarrow \infty} |z_n - w| = 0$$ 그리고 $w = \lim _{n \rightarrow \infty} z_n$이라고 쓴다.실수에서 수렴의 정의와 다른 것은 없지만 복소수의 절댓값의 정의를 생각하면 복소평면 위의 점 $w$에 점점 가깝게 다가가는 것으로 생각할 수 있다.수열의 극한으로 수렴성을 파악하기 어려울 때는 동치인 코시 수열인 지를 알아보는 것도 도움이 된다. 수열 $\{z_n\}$은 이 코시 수열이라는 것은 다음과 같다는 것을 의미한다.\[ |z_n - z_m| \rightarrow 0 \quad \text{as..

정리해서 글을 쓰는 것은 나중에.. 흐름이 눈에 잘 안들어온다.